 (je sais c'est trop laid
:-) )
(je sais c'est trop laid
:-) )
I) Cékoi le principe ?????
Un tunnel freedir (pour la suite, tunnel va etre
mis a la place de truc, c'est plus parlant :-) ) est un effet basé
sur le principe du raytracing ( "lancé de rayons" pour ceux qui
aiment pas l'anglais, et qui se nourrissent a grands coups de multimedia
et d'interactivité : je vous méprise les gars ). Il consiste
à dire que l'ecran est une camera, et donc lancer des rayons par
cette camera, et voir s'ils touchent l'objet rendu (donc s'il y a intersection
entre le rayon et l'objet). Cela est contraire aux lois de la physique,
qui lancerait les rayons d'une source lumineuse et regarderait lesquelles
touchent la camera. Mais bon, on n'est pas des scientifiques, donc on se
contente d'une technique moins rigoureuse, mais qui marche. Une fois qu'on
a determiné s'il y avait intersection, on calcule les coordonnées
du point d'intersection, puis on en déduit le pixel de la texture
a afficher a cet endroit de l'ecran (c'est a dire le mapping). Comme vous
le voyez, le principe est simple, c'est son implémentation qui peut
etre délicate, encore que le tout soit facilement compréhensible
avec des connaissances de bases en mathematiques (vecteurs, resolution
d'equations, ...) et/ou un peu de bon sens (de toute façon y'a les
démonstrations et les résultats). De plus, c'est la même
technique qui est utilisée pour réaliser les raytracers (genre
pov), la différence résidant dans une plus grande rigueur
des calculs, des objets plus nombreux ou complexes, des modeles d'eclairage,
... Mais bon, faut pas compter faire ça en temps réel :-).
Tout ça pour dire que vous pouvez repartir de ça pour coder
un vrai raytracer.
Donc, si je récapitule, le rendu d'un tunnel
freedir se fait comme ceci :
deplacer/tourner la camera;
Une boucle qui balaye
les pixels de la camera (=de l'ecran)
{
calculer un vecteur direction pour ce pixel;
calculer s'il y a intersection entre le rayon et l'objet;
s'il ya intersection
{
calculer les coordonnees du point d'intersection;
mapper la texture sur l'objet en ce point;
}
}
En fait, on ne fait pas le rendu pour chaque pixel,
on se contente de le faire pour 1 pixel sur 64, puis interpoler le tout
(la difference avec un rendu "tout calculé" étant quasi inexistante).
Je vais maintenant reprendre chaque partie de cet algorithme.
II) Variables et types de données utilisés
Donc, si on regarde l'algorithme, de quoi est-ce qu'on a besoin ?
1) la camera :
elle est caracterisée par : - sa position dans l'espace, nous utiliserons
un vecteur à 3 dimensions pour la définir
- son orientation, nous utiliserons une matrice de rotation autour
de x, y et z pour la définir
2) un vecteur de direction : donc un autre vecteur pour ça, mais attention, pour simplifier les choses, ce vecteur sera normalisé ( c'est à dire qu'il aura une norme (longueur) de 1).
3) un rayon : le rayon est lancé par la camera, et sa direction est la meme que le vecteur de direction. Un rayon part donc de la camera, et sera deplacé de 't' fois dans la direction du vecteur direction. L'equation d'un rayon est donc : camera+t*direction. La seule chose le caracterisant sera donc une variable t de type float.
4) une texture : c'est ça qu'on va plaquer (mapper) sur l'objet. Pour simplifier les choses, on prend une texture de 256*256, les coordonnées d'un point se définissant donc par 2 variables de types unsigned char (sur 8 bits).
5) une table pour stocker les resultats, qu'on interpole avant d'afficher a l'ecran : donc là, on aura une table de LARGEUR_ECRAN*HAUTEUR_ECRAN variables point. Point est une structure ayant comme membres x et y (pour stocker les coordonnees du pixel de la texture a afficher).
Les vecteurs sont des structures ayant comme
membres x, y et z, de type float.
Les matrices seront des tableaux de 3x3 float
(précision : dans les moteurs 3d utilisant les matrices, on a souvent
(toujours ?) des matrices 4x4 (on dit alors qu'on a un systeme avec des
coordonnees homogènes je crois :-) ). Les matrices 4x4 dans un espace
a 3 dimensions servent a pouvoir mettre les translations sous forme matricielle,
mais comme la seule matrice utilisée est une matrice de rotation,
on n'a besoin que d'une 3 sur 3).
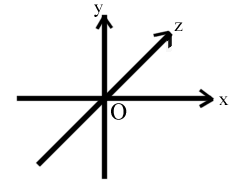
Je précise aussi que le systeme de coordonnées
utilisé est un système de gaucher :
 (je sais c'est trop laid
:-) )
(je sais c'est trop laid
:-) )
Les définitions de types seront donc, en C :
typedef struct
{
float x, y, z;
} VECTEUR;
typedef float MATRICE [3][3]; // matrice 3x3
typedef struct
{
unsigned short x, y;
// on utilise des unsigned shorts sur 16 bits pour l'interpolation
} point;
Et les variables seront :
// camera
VECTEUR camera = { 0, 0, 0 };
// pour que la camera commence a l'origine
MATRICE cam_mat;
// matrice de la camera
// texture 256x256x256
unsigned char texture[65536];
// table de stockage des pixels a afficher
point interpol[321][201];
// ca fait 321x201 au lieu de 320x200 pour l'interpolation (je sais
qu'on peut optimiser en faisant un seul point
// interpol[321*201], mais j'avais la flemme, et c'est moins lisible
apres)
III) Déplacer/tourner la camera
Donc la c'est tout simple, pour déplacer la
camera, on fait des petits :
camera.x = truc;
camera.y = machin;
camera.z = couille_de_loupe;
Ou alors on ajoute des valeurs aux coordonnées
de la camera.
Dans les deux cas, il faut faire gaffe que la camera
sorte pas de l'objet, sinon ça fait crade.
Moi, ma camera se déplace de 'vitesse' unités
sur z, et je calcule ses coordonnées x et y comme ça :
camera.x = (80*cos(alpha/2)
+ 60*sin(alpha/3));
camera.y = (100*sin(alpha/4)
+ 40*cos(alpha));
alpha += .26;
// alpha est un float
camera.z += speed;
Un peu plus compliqué pour tourner la camera.
J'utilise 3 variables float rotx, roty et rotz définissant les angles
de la rotation de la camera, auxquelles j'ajoute une constante a chaque
nouvelle image. Ensuite, je recalcule la matrice de rotation en fonction
de ses 3 variables.
Pour calculer la matrice de rotation, on peut allegrement
réutiliser cette "formule", qui resulte d'une multiplication a la
main des matrices de rotations autour de x, y et z :
m[0][0] = cosy*cosz;
m[0][1] = cosy*sinz;
m[0][2] = -siny;
m[1][0] = sinx*siny*cosz - cosx*sinz;
m[1][1] = sinx*siny*sinz + cosx*cosz;
m[1][2] = sinx*cosy;
m[2][0] = cosx*siny*cosz + sinx*sinz;
m[2][1] = cosx*siny*sinz - sinx*cosz;
m[2][2] = cosx*cosy;
Vous pouvez aussi recalculer vous-même...
Cette matrice est ensuite appliquée au vecteur
de direction pour lancer le rayon ( par multiplication de la matrice et
du vecteur direction).
IV) Calculer un vecteur direction pour chaque pixel
Comme je l'ai écrit plus haut, on ne fait
pas un calcul pour chaque pixel, mais 1 sur 8 en x et 1 sur 8 en y (donc
1/64 au total). Ca va donner un truc comme ca dans le code :
for(y=0;y<=200;y+=8)
for(x=0;x<=320;x+=8)
{
...
}
Une fois qu'on connait par quel pixel on lance le
rayon, c'est simple de trouver les coordonnées du vecteur direction.
On commence par calculer la direction sans tenir compte de l'orientation
de la camera (comme si la camera etait orientée selon l'axe des
z), puis on multiplie ce vecteur par la matrice de la camera, et enfin
on le normalise.
Pour calculer le vecteur direction avec une camera
"droite", on fait comme ceci :
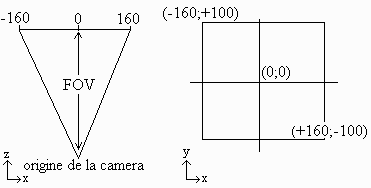
soit :
direction.x = ((float)(x-160))/FOV;
direction.y = ((float)(y-100))/FOV;
direction.z = 1;
Ensuite, on multiplie ce vecteur par la matrice de
rotation, soit, pour ceux qui ne sont pas à l'aise avec le calcul
matriciel :
direction.x = direction.x*cam_mat[0][0]
+ direction.y*cam_mat[0][1] + direction.z*cam_mat[0][2];
direction.y = direction.x*cam_mat[1][0]
+ direction.y*cam_mat[1][1] + direction.z*cam_mat[1][2];
direction.z = direction.x*cam_mat[2][0]
+ direction.y*cam_mat[2][1] + direction.z*cam_mat[2][2];
A ce stade, on a donc un vecteur direction, qui
pointe dans la bonne direction en tenant compte de l'orientation de la
camera. Il nous reste donc a le normaliser, c'est à dire ramener
sa norme à 1. La norme d'un vecteur U est donnée par la formule
(démontrable avec le théorème de notre pote Pythagore)
: ||U|| = racine(Ux²+Uy²+Uz²). Donc, pour ramener cette
longueur à 1, il faut diviser chaque coordonnée par la longueur,
soit, en C :
float norme;
norme = sqrt(u.x*u.x + u.y*u.y + u.z*u.z);
// l est la norme du vecteur u
u.x /= norme;
u.y /= norme;
u.z /= norme;
Voila, on est en mesure de calculer un vecteur normalisé de direction pour chaque pixel de l'écran. Reste maintenant à le lancer, et c'est maintenant qu'on passe à la partie marrante (je trouve).
V) Calculer s'il y a intersection entre le rayon et l'objet
Cette partie sera subdivisée en 3 parties, traitant chacune les calculs pour l'intersection d'un rayon avec respectivement un tunnel, une sphère et un plan.
A) Calculer l'intersection entre un rayon et un tunnel
Là aussi, il faut faire appel aux maths. Qu'est-ce
qu'un tunnel ? C'est simplement un cylindre, doncune succession de cercles
concentriques le long de l'axe des z (ou n'importe quel autre, pas forcément
un des axes de coordonnées, mais ça simplifie les calculs).
On a donc notre direction, notre caméra et notre rayon sous le bras,
et on va chercher s'il y a intersection. L'equation du rayon est, comme
vu plus haut, camera + t*direction (pour chaque coordonnée
bien sur). Il faut donc chercher s'il y a intersection, et si oui, la valeur
de t.
Le tunnel est une succession de cercles, et que
nous dit Pythagore sur les cercles ? Tout simplement que, pour un cercle
centré sur l'axe des z, x²+y² = r² (avec r
le rayon du cercle). Il reste donc à substituer aux x et y de cette
égalité les coordonnées du rayon. Il y a donc intersection
si :
(camera.x + t*direction.x)² + (camera.y + t*direction.y)²
= r²
Ce qui equivaut à (en développant):
camera.x² + 2*t*direction.x*camera.x + t²*direction.x²
+ camera.y² + 2*t*direction.y*camera.y + t²*direction.y²
- r² = 0
Ensuite on factorise par t et t², pour aboutir
à :
(direction.x²+direction.y²)*t² + (2*(direction.x*camera.x
+ direction.y*camera.y))*t + (camera.x²+camera.y²-r²) =
0
Regardez bien la ligne d'au-dessus... Ooooh, magie,
c'est une équation du second degré, facile a résoudre
pour quelqu'un qui a un niveau de premiere en maths. Petit rappel, pour
résoudre une équation de la forme ax²+bx+c=0, on calcule
d'abord son discriminant delta=b²-4ac.
Si delta>0, alors l'équation admet 2 solutions, qui sont :
-b - racine(delta)
-b + racine(delta)
x1=-------------------------
et x2=-----------------------------
2a
2a
Si delta=0, alors l'équation admet une seule solution :
-b
x=---------
2a
Et enfin, si delta<0, l'équation n'a pas de solution.
Donc, pour savoir s'il y a ou non intersection, on
calcule :
a = direction.x²+direction.y²;
b = 2*(direction.x*camera.x
+ direction.y*camera.y);
c = camera.x²+camera.y²-r²;
Et on résout l'equation comme vu précédemment.
Une fois que l'equation est résolue, on a 1 ou 2 't' réponses,
si on en a un seul, pas de problème, si on en a 2, il faut prendre
le positif (ce qui veut dire, en reprenant l'équation du rayon,
que le point d'intersection a lieu devant la camera).
note : le c de l'équation (camera.x²+camera.y²-r²) est constant pour toute l'image, car direction n'intervient pas dedans, donc on peut accelerer (tres) legerement le calcul en le sortant de la boucle principale.
B) Calculer l'intersection entre un rayon et une sphère
Le calcul d'une intersection sphère/rayon est quasiment pareil que celui du tunnel. On prend une sphere centrée sur l'origine du repère, et toujours d'après Pythagore, il y a intersection quand : x²+y²+z² = r².
(pour que ca reste lisible, j'écris cx à
la place de camera.x et dx à la place de direction.x)
Soit, en y substituant l'équation du rayon
:
(cx + t*dx)² + (cy + t*dy)² + (cz + t*dz)² = r²
On développe...
cx² + 2*t*dx*cx + t²dx² + cy² + 2*t*dy*cy + t²dy²
+ cz² + 2*t*dz*cz + t²dz² - r² = 0
On met t et t² en facteur :
(dx² + dy² + dz²)t² + (2*(dx*cx + dy*cy + dz*cz))t
+ (cx² + cy² + cz² - r²) = 0
Et hop ! Encore une chtite équation du second
degré, qu'on s'empresse de résoudre en faisant :
a = direction.x*direction.x + direction.y*direction.y
+ direction.z*direction.z;
b = 2*(direction.x*camera.x + direction.y*camera.y
+ direction.z*camera.z);
c = camera.x*camera.x + camera.y*camera.y + camera.z*camera.z
- r*r;
Après, il ne reste qu'à résoudre comme on l'a vu dans le paragraphe précédent...
C) Calculer l'intersection entre un rayon et un plan
En fait, j'ai écrit un plan, mais la plupart
du temps, on voit 2 plans, et comme ça rend mieux et que c'est en
fin de compte la même chose, on va voir comment faire avec 2 plans.
D'abord, un petit schéma pour se fixer les
idées :
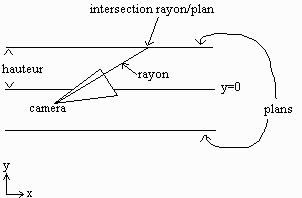
Donc, on peut déja dire que si direction.y
est positif, il y a une intersection avec le plan du haut, et s'il est
négatif, avec le plan du bas. Ensuite, c'est tout simple, il y a
intersection quand |camera.y+t*direction.y| = hauteur. On éjecte
la valeur absolue en prenant chaque cas séparement (direction.y
positif ou négatif). Ensuite, on trouve t tout simplement par :
t = (hauteur-camera.y)/direction.y;
// quand direction.y>0
VI) Calculer les coordonnées du point d'intersection
Une fois qu'on a t, le point d'intersection est facile
a trouver, il suffit de le remplacer dans l'équation du rayon :
intersection.x = camera.x
+ t*direction.x;
intersection.y = camera.y
+ t*direction.y;
intersection.z = camera.z
+ t*direction.z;
C'est tout ! :-)
VII) Mapper la texture sur l'objet
Le mapping consiste a trouver quel pixel de coordonnées
(u;v) de la texture on va afficher en fonction du point d'intersection
trouvé.
Comme pour le V), cette partie est composée
d'une partie pour chaque type d'objet.
A) Mapping de texture sur un tunnel
La texture est plaquée sur un cylindre, elle "s'enroule" autour.

Mais puisque nous sommes sur un cercle, on trouve
facilement que alpha = tan^-1(intersection.x/intersection.y).
Donc, comme la texture est une 256x256 :
u = 256*atan2(intersection.x,
intersection.y) / PI;
v = intersection.z;
Note : atan2(x, y) correspond en théorie à atan(x/y), mais la fonction atan de la libc est buggée. De plus, il faut faire gaffe de pas diviser par 0, donc dans la pratique on ajoute une valeur toute petite à intersection.y.
B) Mapping de texture sur une sphère
Là, pour trouver v, c'est la même chose que le u du tunnel.Sinon, en utilisant le fait que sinus = coté opposé/hypoténuse, on trouve u.
u = asin( (intersection.y)
/ rayon )*128+128;
v = 256 * atan2(intersection.z,
intersection.x) ) /PI );
C) Mapping de texture sur un plan
Là, ça tombe dans l'évidence,
je pense que j'ai pas besoin de donner d'explications et que je peux directement
vous donner :
u = intersection.x;
v = intersection.z;
VII) Interpolation de la table et affichage
Pour l'interpolation de la table, je pense que je
ne peux pas mieux l'expliquer que cyg/blabla, donc je mets sa doc ici,
et pour ceux qui comprennent pas, y'a une implémentation dans le
source. Une fois que la table est interpolée, c'est fini !!!! On
peut afficher pour chaque pixel de l'ecran le pixel de la texture qui correspond.
Comme la texture est en 256x256, et qu'elle est stockée dans un
tableau de 65536 (2^16) octets, le pixel de coordonnées (x;y) est
texture[( (y<<8)+x ) &0xffff] (ca correspond a 256*y+x quoi :-)
).
Donc l'affichage se fait simplement par :
for(y=0;y<200;y++)
for(x=0;x<320;x++)
{
c = tex[((interpol[x][y].y<<8)+interpol[x][y].x)&0xffff];
putpixel(x, y, c);
}
VIII) Le truc à ripper !!!!
Bon, je file en cadeau bonus extra plus top mon propre programme de machins freedirs, avec le source. Il s'agit bien sûr d'une version "brute", sans les petits plus qu'il faudrait dans une démo, mais je suppose que c'est suffisant pour comprendre le truc (je sais, c'est fait avec allegro, allegro ça pue du cul, mais bon, j'oblige personne à mater le source).
--> Le programme
<--
--> Le source
<--
Note sur le programme : donc le prog génère une texture,
pis affiche un tunnel, une sphere ou des plans. Pour changer l'objet rendu,
on fait F1, F2 ou F3. La vitesse est reglable avec les touches + et -.
Enfin, ya un petit truc affiché en haut à gauche, c'est ce
qu'on calcule réellement : un rectangle de 40*25 (c'est à
dire qui n'est pas obtenu par interpolation). On desactive ça avec
backspace.
IX) Quelques idées d'améliorations
Bon, donc je vais vous livrer des idées que j'ai pour rendre ça un ptit peu plus joli (mais vous chercherez l'implementation tout seul bande de feignasses ! :-) ) :
-on peut gérer la
lumiere, en affichant un pixel en fonction de son éloignement (c'est
à dire t)
-on peut faire des déformations
de tunnel comme dans saint/halcyon, en calculant le rayon du tunnel a chaque
nouveau rayon, en fonction du vecteur direction
-y'a un autre truc sympa,
c'est d'interpoler 2 tunnels, on a l'impression qu'ils fusionnent
-écouter bérurier
noir toute la journée
-gérer les refractions,
reflexions et toutes ces choses marrantes
-là je sais pas du
tout si c'est possible (pour des questions de vitesse en fait), mais on
peut essayer de faire un tore freedir
-...
X) Les trucs de la fin dont tout le monde se fout sauf l'auteur
Bon, je vais faire quelques remerciements/greetings,
d'abord à kombat, l'auteur de la doc de laquelle je suis parti avant
de coder cet effet, et cyg/blabla, l'auteur de la doc sur la bi-interpolation
linéaire. Sinon, un petit coucou au passage à tous #codefr,
et plus particulièrement piaku, starman, lord_k, kwa, dbug, et u2.
Pour ceux qui veulent plus de renseignements, vous pouvez m'envoyer un
mail, ou venir me causer sur #codefr, #demofr ou #pixelfr (pour ce dernier
chan, vous posez vos questions en query :-) ), tous les 3 sur IRCnet. Mon
adresse mail c'est : chewie@wanado.fr
Voilà, je crois que c'était tout ce que j'avais à
dire... Au fait, ça me fait toujours autant plaisir d'écrire
des docs, et je conseille à tous les coders de faire ça,
plutôt que de se contenter de dire qu'ils explosent tout le monde...
Sinon, tout est libre de droits hein, je vais pas
faire l'enculé, donc si vous voulez diffuser, copier, modifier,
ripper ... vous avez le droit, même sans ma permission (même
sur une plate-forme pétrolière ! :-) ). Hakim Bey spirit
rulez