Cet effet graphique très à la mode dans les démos il y a quelques années est assez facile à coder. La partie la plus complexe est d'essayer de comprendre ce qui se passe derrière l'algorithme pourtant très simple. En passant, les notions présentées dans ce chapitre sont communes à celles du chapitre 4 de la section 3D. En effet, nous allons traiter de lumière et de modèles d’illumination, ainsi que des normales de surfaces. On assume ici que le lecteur connaît ces bases théoriques.
Comme expliqué dans ce tuteur, pour effectuer de l'ombrage, on a besoin du produit scalaire entre la normale de surface et le vecteur de lumière normalisé, et multiplier on doit multiplier le tout par la lumière diffuse. En modifiant la normale de surface sur un point donné, nous changeons aussi l'ombrage de ce point. Le bump mapping se base sur ce principe, excepté que nous ne voulons pas connaître les normales de chaques pixels, mais plutôt leurs signes (pseudo-normales).
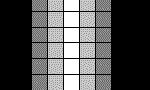
Notre effet doit avoir lieu sur un tableau 2D contenant des valeurs représentant la "hauteur" des points, exactement comme on ferait pour du voxel spacing. Cette "bumpmap", ou "carte de bosses" pourrait ressembler à ceci:

Comme vous voyez, les pixels en tons de gris représente la "hauteur" des pixels, blanc étant le plus haut et noir étant le plus bas. Il faut à présent calculer leurs "pente", afin de savoir s'il montent ou s'ils descendent. Pour se faire, il s'agit de vérifier leurs voisins, et de déterminer le signe. Voici le coeur du bump mapping:
Xd = bumpmap[U+1][V] - bumpmap[U-1][V]
Yd = bumpmap[U][V+1] - bumpmap[U][V-1]
Vue de côté, cette même échantillon pourrait avoir l'air de cela:
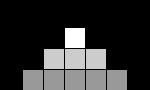
Maintenant, pour obtenir le vecteur qui va venir modifier notre normale de surface, nous normalisons avec ces nos pseudo-normales Xd et Yd. La normale Z est celle qui représente directement la "hauteur" du pixel:
Nx = Xd
Ny = Yd
Nz = max( 1 - sqrt(Ny ^ 2 + Nx ^ 2 ) , 0 )
longueur = sqrt( Nx ^ 2 + Ny ^ 2 + Nz ^ 2)
Nx /= longueur
Ny /= longueur
Nz /= longueur
En procédant de la sorte, nous modifions la géométrie de la surface, en simulant des variations en hauteur des points sur la surface en modifiant l'ombrage. Bien que les calculs pour se faire ne sont pas trop demandant, il faut quand même procéder de la bonne façon. Également, on assume que la bumpmap est de la même taille que l'écran (dans notre cas, 320x200), et que le vecteur de lumière est directement en face de l'écran à (0,0,-1).
La première chose que l'on peut faire est de précalculer la normale nZ, le 1 - sqrt(Ny ^ 2 + Nx ^ 2 ). La façon la plus commune est d'utiliser un tableau d'une taille très pratique, 256x256, ce qui veut dire que l'on peut précalculer des valeurs pour des valeurs allant entre-128 à 127:
float z[256][256];
float tx,ty;
for (int x=-128;x<128;x++)
for (int y=-128;y<128;y++)
{
tx=x/128;
ty=y/128;
z[x+128][y+128] = max( 1 - sqrt(tx*tx + ty*ty) , 0);
}
Ce tableau précalculer est en fait ce qu'on appelle une Environment map. On l'utilise souvent pour simuler la réflexion de l’environnement sur une surface (ie : un mirroir) ou pour faire du "faux" phong shading. En effet, du vrai phong shading demande beaucoup de calculs et est difficilement adaptable pour les graphiques en temps réel.
Comme on connaît la normale de surface pour un point donné dans l'environment map, il n'est pas difficile de précalculer le produit scalaire de cette normale, et d'en calculer, a partir d'une source de lumière, la couleur résultante.
void EnvMap()
{
float nX,nY,nZ;
for (int y=0;y<256;y++)
for (int x=0;x<256;x++)
{
nX=(x-128)/128.0;
nY=(y-128)/128.0;
nZ=1-sqrt(nX*nX+nY*nY);
if (nZ<0) nZ=0;
// Phong = ambient + dif*dot + dot^2 * spec
envmap[x+y*256]=AMBIENT+(byte)min(255,(nZ*DIFFUSE+nZ*nZ *SPECULAR));
// Lambert = ambient + diffuse * angle
// envmap[x+y*256] = AMBIENT + DIFFUSE * nZ;
}
}
Ici je présente deux modèles d'illumination possible: le Lambert Shading et le Phong Shading (mais via du Environment mapping).Nous devons prendre en considération la position de la source de lumière dans nos calculs, et ajuster ses cordonnées pour s’assurer quelle soit considérée comme l'origine (ie: x et y += 128). Voici la fonction principale:
void Bump(int lx,int ly)
{
int nx,ny; // les pseudo-normales
// Ajuster la source lumineuse pour qu'elles soient à l'origine
lx+=128;
ly+=128;
int offset=0;
for (int y=0;y<200;y++)
{
for (int x=0;x<320;x++)
{
// Obtenir la "pente" de la bumpmap
nx=bumpmap[offs+1]-bumpmap[offs-1];
ny=bumpmap[offs+320]-bumpmap[offs-320];
// Ajustement de la normale d'après la source lumineuse
nx-=(x-lx);
ny-=(y-ly);
// On s'assure qu'on ne dépasse pas l'envmap
if (nx>255 || nx<0) nx=255;
if (ny>255 || ny<0) ny=255;
// Ramene la couleur de l'envmap dans le buffer
buffer[offset++]=envmap[nx+ny*256];
};
};
}
Il ne reste plus qu'a mettre sur pied une palette correspondante. L'effet est très intéressant, et offre beaucoup de possibilité (on utilise le même principe pour simuler l'eau). Je présenterai également bientôt l'effet de simulation de surface aqueuse, avec ombrages et réflexions. Cet effet se réalise également en 3D.